Königsberg a Teorie Grafů: Jak Eulero Změnil Pohled na Matematiku
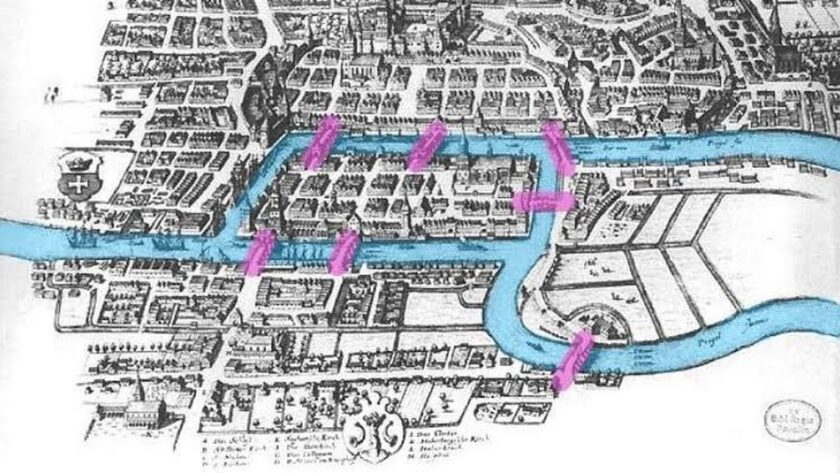
Město pruského původu Königsberg (dnes Kaliningrad v Rusku) bylo protknuto řekou Pregel a spojeno sedmi mosty, které spojovaly dvě ostrovy a protilehlé břehy, čímž město rozdělovaly do čtyř zón. Legenda vypráví, že mezi obyvateli koloval podivný zvyk: najít trasu, která by vedla přes všechny mosty jednou. Nápad byl jednoduchý, ale nikomu se nedařilo úspěšně tuto výzvu splnit.
Otázka skončila v rukou matematika Leonharda Eulera. Zpočátku nebyl Euler přesvědčen, že by se jednalo o skutečný matematický problém, ale při pohledu na mapu města dostal rozhodující intuici: nezáleželo na tom, jak se lidé pohybovali mezi čtyřmi zónami města (označenými jako A, B, C a D), ale pouze na pořadí, ve kterém překonávali mosty.
Odtud pochází Eulerova brilantní zjednodušení: představit si pozemní části jako body a mosty jako čáry. Problém tak mohl být schématizován následujícím způsobem:
Bez toho, aby si to uvědomil, Eulero vytvářel základ nové disciplíny, teorie grafů, která je dodnes zásadní pro studium schémat, jež mohou být redukována na prvky a spojení. Graf je jednoduchý způsob, jak reprezentovat spojení: skládá se z bodů (nazývaných uzly) a čar, které tyto body spojují (označovaných jako hrany).
Při analýze systému zjistil, že možnost projít všechny mosty jednou závisí výhradně na počtu čar, které “dotýkají” každého bodu, tedy na stupni uzlů. Tato cesta – dnes známá jako eulerovský tah – je možná pouze tehdy, když:
- všechny uzly mají sudý stupeň (tedy sudý počet čar spojených s bodem), nebo
- přesně dva uzly mají lichý stupeň (výchozí a cílový bod).
Problém? V Königsbergu měly všechny čtyři uzly lichý stupeň. Jinými slovy, městská výzva byla od začátku nemožná.
Ironií osudu by jediný způsob, jak učinit hlavolam řešitelným, byl odstranit alespoň jeden z mostů. K tomu opravdu došlo, ale tragickým způsobem: během druhé světové války byla část města a některé mosty zničeny bombardováním, než se Königsberg přeměnil na dnešní Kaliningrad.
Eulerovo řešení však přežilo více než původní mosty. Tento jednoduchý městský hlavolam dal impuls teorii grafů a obecně novému způsobu uvažování o formách a spojení, čímž otevřel cestu moderní topologii.